


If such a number L exists, we usually denote it by ƒ'(w). More specifically, to say that ƒ: U → C is differentiable at an interior point w in U means the following: there exists some complex number L such that for every real number ε > 0 there exists a real number δ > 0 with the property that for all complex numbers z in U with 0 < |z - w| < δ, we have |/ - L| < ε. Holomorphic functions are central in the theory of complex functions. If ƒ is differentiable on an open set U, one also says that ƒ is holomorphic on U, or sometimes that ƒ is analytic on U. If U is open, and if ƒ is differentiable at every point of U, we say that ƒ is differentiable on U. If the limitĮxists, we say that ƒ is (complex) differentiable at w, and we denote the value of this limit by ƒ'(w). Suppose further that ƒ: U → C is a complex-valued function defined on U, and suppose w is an interior point of U. Let C denote the set of complex numbers, and suppose U is some subset of C. Did you mean to ask about the differentiation of complex-valued functions defined on subsets of the complex plane? Such functions may (sometimes) be differentiated. Since a complex number in itself is a constant, its derivative is zero. They seem to get the point across very efficiently. You may want to review some of Sal's videos on derivatives - especially the ones where he graphs the derivatives intuitively. In sum, basically, the chain rule takes into consideration of how the functions within a function determine the function's slope at some input. That's the only time you will make sense of it all. Even when the slope of f(x) is 0 at x = -2, we see the graph of the derivative crosses the x-axis at x = -2.Ī lot of this has to do with looking at a graphs of a function and their derivatives on the same graphing sheet. we see that the x-value produces an incredibly negative y-value, which is the slope of the function f(x) at the x-value of interest (sometimes called a). and we know the derivative is decreasing. Towards the top of of the parabola on the left side, it almost looks like a straight line. then, if you graph 8x+4 on the same sheet of graphing paper. If you graph (2x+1)^2 you will see that it is a parabola. And there are other functions that can be written both as products and as compositions, like d/dx cos(x)cos(x).When you apply the chain rule, you're taking into account how the slope of the function is behaving by the influence of the internal variables. There are other functions that can be written only as products, like d/dx sin(x)cos(x). In summary, there are some functions that can be written only as compositions, like d/dx ln(cos(x)).

recognizes that we can rewrite as a composition d/dx cos^2(x) and apply the chain rule. You can see this by plugging the following two lines into Wolfram Alpha (one at a time) and clicking "step-by-step-solution":įor d/dx sin(x)cos(x), W.A. This suggests that the problem we are about to work (Problem 2) will teach us the difference between compositions and products, but, surprisingly, cos^2(x) is both a composition _and_ a product. Immediately before the problem, we read, "students often confuse compositions. The placement of the problem on the page is a little misleading. Yes, applying the chain rule and applying the product rule are both valid ways to take a derivative in Problem 2.
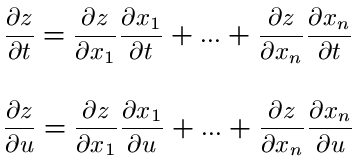
For example, cos ( x 2 ) \greenD f ′ ( g ′ ( x ) ) start color #11accd, f, prime, left parenthesis, end color #11accd, start color #ca337c, g, prime, left parenthesis, x, right parenthesis, end color #ca337c, start color #11accd, right parenthesis, end color #11accd.


 0 kommentar(er)
0 kommentar(er)
